Note: This is not a flat-earth article. It proves that no flat-earth model, no matter how sophisticated and accurate it is, can ever be as good as the round-earth model.
I think most of us are aware by now that a large and increasing number of people believe that the Earth is flat. The flat earthers, as they are called, consist of a wide variety of people from different backgrounds, and they preach a wide variety of flat earth theories. There is only one thing that they all have in common: a genuine lack of trust in all space agencies.
Most round earthers dismiss the flat earthers as raving lunatics, without trying to think too hard about it. At the same time, the flat earthers mock the ignorance and complacency of the round earthers. Whenever members of both groups get into an argument, it becomes clear that neither group can convince the other of anything.
No common ground
The main argument the flat earthers use is the argument from the senses. The Earth looks and feels flat, therefore the Earth must be flat. But the round earthers don’t accept this argument. The earth is so big, they say, that it is not surprising that the relatively tiny area that we experience looks flat. In fact, it looks and feels exactly as we would expect, so the flat earthers’ argument from the senses is unconvincing.
The round earthers, for their part, come up with all kinds of arguments based on the principles of mainstream physics and astronomy. But flat earthers often reject those principles by pointing out the assumptions involved, or more commonly by simply refusing to trust the scientific authorities. These types of arguments usually don’t change the minds of hard core flat earthers.
The reason flat earthers and round earthers can’t agree on anything is because they have no common ground. Their philosophies tend to live in completely disjoint realms of physical understanding. Flat earth physics is nonsense to the round earthers, and round earth physics is foolish dogma to the flat earthers.
In time, the truth will be found. Flat earthers, after incorporating more and more precise observations, should eventually converge on a unified flat earth theory. This theory will be identical to the current round earth model, except modified by a nonlinear spatial transformation.
The flat-earth/round-earth correspondence
It turns out that it is relatively easy to build a flat earth model that agrees with all scientific observations. All we have to do is take the current round earth model and transform it to make it look flat.
The round earth fits nicely into a spherical coordinate system defined by the parameters ,
, and
. The parameter
represents the radial distance from the center of the earth,
represents the polar angle measured from the zenith (or the north pole), and
is the azimuthal angle. A diagram of the round earth embedded in this coordinate system is shown in the figure below.
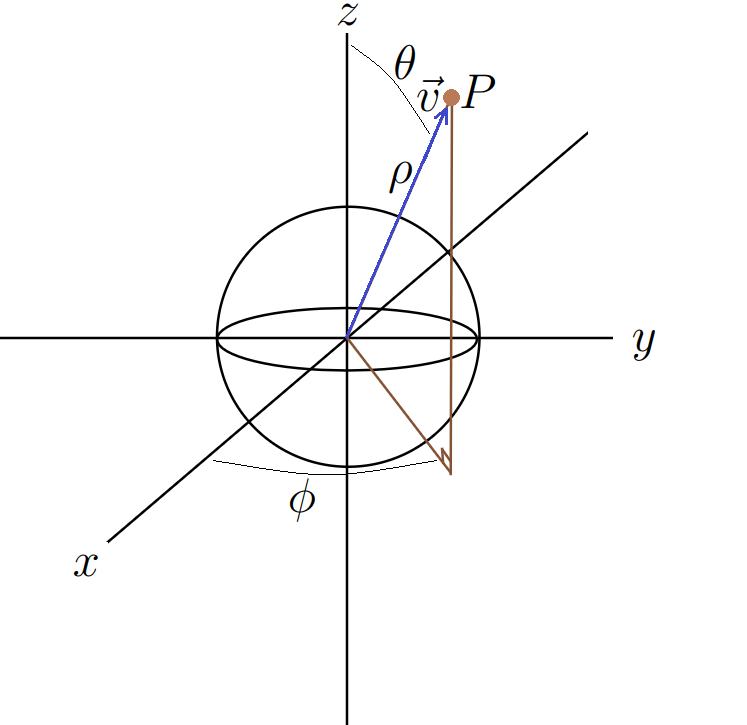
The vector points from the origin to a single point
. The vector
can be expressed in spherical coordinates as follows:
We can apply a transformation to the point and every other possible point to make the earth look like a flat disk embedded in a cylindrical coordinate system defined by
,
, and
. The transformation maps
to
, or in other words
to
, as follows:
where
The coordinate parameter is the same as in the spherical case, the parameter r is the distance from the z-axis, and z is the vertical position measured by the z-axis. The radius of the round earth and the radius of the flat earth are denoted by
and
, respectively. The parameter k controls the exponential compression of space. This transformation maps the entire universe to a hemisphere over the flat earth. A diagram of this flat earth is shown below.
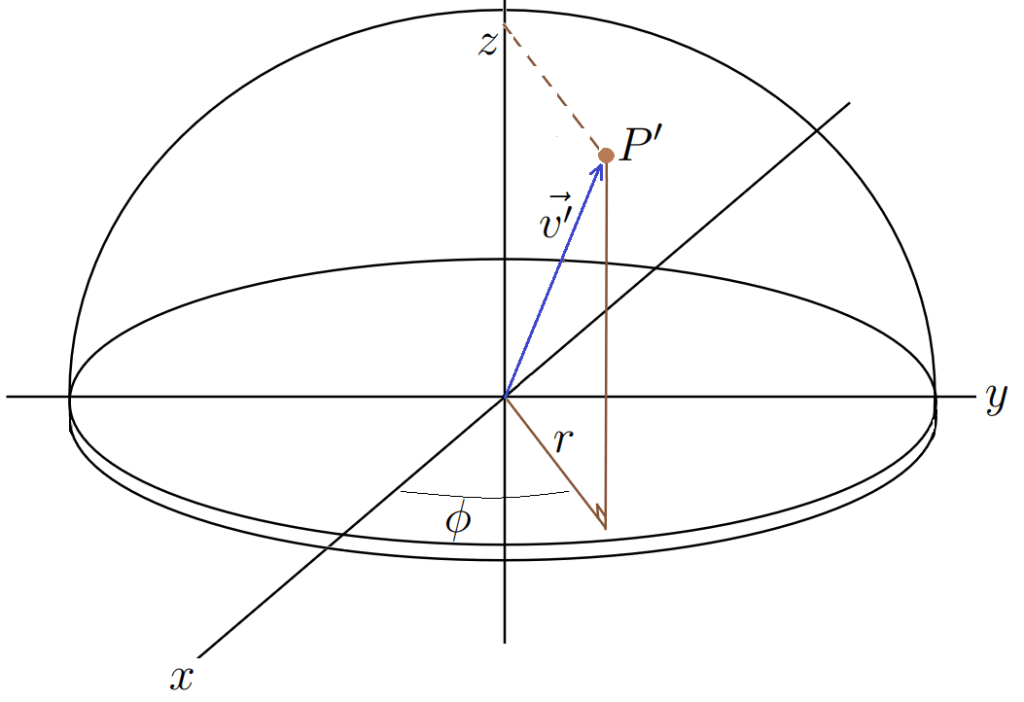
This looks very similar to today’s most popular flat earth theories. The Earth is viewed as a flat round disk, with the north pole in the center, and Antarctica making a ring around the outer edge. The sun and moon appear to circle around the north pole above the equator, while the stars appear to be stuck on a hemispherical firmament over the earth.
But this is intrinsically identical to the round earth, just viewed in an inconvenient way that doesn’t help our physical intuition. Our brains are trained to view the world in flat space, but this space is now strongly curved. It is rotated, stretched in some directions, squished in others, and mind-bendingly difficult to comprehend. Although consistent theories of physics can be constructed in this model, they would necessarily be very complicated.
Every physical law in this flat earth model must take into account the extrinsic curvature that we have aggressively imposed upon space. Because of this curvature, all physical laws will vary depending on the position relative to the Earth’s North Pole. Light rays don’t travel in straight lines in this model, which is why the Earth would appear to be round when viewed from space. As you head farther south, space is stretched in the east-west direction and shortened in the north-south direction. The effects of this curvature are not noticeable to those living in this universe, so we would all be “deceived” into thinking that the Earth is actually round. The extrinsic curvature could only be observed by someone living outside of this universe. That is what makes it “extrinsic.”
Duality in physics
The flat-earth/round-earth correspondence that we have just demonstrated brings up an important concept in Physics and Mathematics called “duality.” Duality denotes the intrinsic equivalence of seemingly different mathematical representations of the same underlying system. It has become a huge topic in theoretical physics in the last few decades. The hype began with the discovery that 5 different competing string theories were all related. Each string theory could be transformed into another, and the predictions from one would correspond to the predictions in the other.
Duality became front page news again in the physics world with the discovery of the AdS/CFT correspondence. This duality occurs between a specific version of string theory in a 5-dimensional anti-deSitter space (AdS) and a Conformal Field Theory (CFT) on the 4-dimensional boundary of that space. Predictions in one theory can be mapped to predictions in the other. What makes this particular duality especially interesting is that the 5-dimensional model includes gravity, while the 4-dimensional model does not, indicating that it might be possible to explain gravity as a holographic projection of a quantum field theory on a lower-dimensional space.
Dualities in physics are really dualities in mathematics. They arise because the underlying logic of the mathematical structures turns out to be the same. Dualities can be useful, because problems that are difficult in one theory may be easier in a dual theory. Dualities can also shed light on the assumptions that we are making in the construction of our theories.
In the case of the flat-earth/round-earth correspondence, the equivalence of the two theories is easy to see. One is simply a spatial transformation of the other. The assumption that goes into the round-earth model is that space has zero extrinsic curvature. In other words, the universe isn’t squished and squeezed and stuffed into some higher, more fundamental space. Since both theories are equivalent in every way except for the extrinsic curvature, and this parameter has no observable effects, it follows that both theories will produce equivalent predictions.
Occam’s Razor
None of the popular flat earth models today have nearly as much explanatory power as the mainstream round earth paradigm, but the model I just invented does. The flat earthers might eventually figure it out. Does this mean that we round earthers wrong then? Can we not prove the earth is round after all?
It turns out, there are no physical experiments that can be done to disprove this flat earth theory. The real reason we accept the round earth model is not because of logic alone, but because of Occam’s Razor. Occam’s Razor is not really a logical proof, but just a practical rule. It states that whenever two competing theories have equal explanatory power, we should choose the simpler one. There are infinitely many theories that can explain everything just as well as the mainstream theories, but the mainstream theories are the simplest explanations we have found, with minimal assumptions involved.
Any consistent flat earth theory that agrees with observations must assume a complicated and unexplained extrinsic curvature of the universe. It is a physically irrelevant parameter (it doesn’t affect experiments), but including it makes the math much harder. Everything is more difficult to understand in this model. Even the simplest physical laws, such as Newton’s laws, become incredibly difficult to manage. Why would anyone want to use this model when a much simpler one is available?
The only curvature we deal with in the round-earth model is intrinsic curvature, which causes observable effects that we can measure, and cannot be arbitrarily removed by choice. Even in my flat-earth model, the earth would retain the effects from a hidden spherical geometry.
One day, in the distant future, an intelligent flat earther might realize that transforming the complicated flat-earth physics into a round-earth version makes the math much easier. They might call it a mathematical trick, rather than a physical reality, as was done with the heliocentric model of Copernicus five hundred years ago. Hopefully, they will apply Occam’s Razor and finally reject the overcomplicated flat-earth model.


